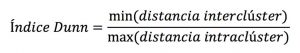Before starting to explain what Clustering is all about, let’s look at an example.

A bank wants to give credit card offers to its customers. Today, they examine the details of each customer and, based on this information, decide which offer to make to which customer.

Now the bank may potentially have millions of customers, so does it make sense to look at the details of each customer separately and then make a decision? Of course not. This would be a manual process and would take a great deal of time.

So what can the bank do? One option is to segment your customers into different groups, for example, the bank can group customers based on their income: high income, average income, low income.

The bank can now make three different strategies or offers, one for each group. Here, instead of creating different strategies for individual clients, they only have to make 3 strategies. This will reduce effort as well as time.

The three groups formed are known as clusters and the process of creating these groups is known as clustering.

Formally, we can say that clustering is the process of dividing all data into groups, also known as clusters, based on patterns in the data .

Clustering or grouping is one of the most used forms of Unsupervised Learning . It’s a great tool for making sense of unlabeled data and for grouping data into similar groups.

A clustering algorithm can decipher structures and patterns in a data set that are not apparent to the human eye. Overall, clustering is a very useful tool to add to your machine learning toolset.

What is a cluster?

Cluster is the collection of data objects that are similar to each other within the same group, class, or category and are different from the objects in the other clusters.

Grouping is an Unsupervised Learning technique in which there are predefined classes and prior information that defines how data should be grouped or labeled into separate classes. It could also be considered as an exploratory data analysis process that helps us uncover hidden patterns of interest or structure in the data.

Clustering can also function as a stand-alone tool to gain insights into data distribution or as a preprocessing step in other algorithms.

Cluster Properties

Let’s take the same example of the bank, mentioned above. For simplicity’s sake, let’s say the bank only wants to use revenue and debt to do the segmentation. They collected customer data and used a scatter plot to visualize it:

On the X axis, we have the client’s income and the Y axis represents the amount of debt. Here, we can clearly visualize that these customers can be segmented into 4 different groups.

This is how clustering helps to create segments or clusters from the data. In addition, the bank can use these clusters to strategize and offer discounts to its customers. So let’s look at the properties of these groups.

Property 1

All data points in a cluster must be similar to each other. Let’s see this in our example.

If the customers in a particular group are not similar to each other, then their needs may vary. If the bank makes them the same offer, you may not like it and your interest in the bank may be reduced, so it’s not ideal.

Having similar data points within the same cluster helps the bank use targeted marketing. You can think of similar examples from your daily life and think about how clusters will impact or already impact business strategy.

property 2

The data points of the different groups should be as different as possible. This will make sense intuitively if you grasped the property above. Let’s take the same example again to understand this property. Which of these cases do you think will give us the best groups?

If you look at case 1, the customers in the green and blue groups are very similar to each other. The first three points in the green group share similar properties as the first two customers in the blue group. They have high income and high debt value. Here we have grouped them differently.

Whereas, if you look at case 2, the points in the green group are completely different from the customers in the blue group. All customers in the blue cluster have high income and high debt, and customers in the green cluster have high income and low debt value. We clearly have a better customer pool in this case.

Therefore, data points from different clusters should be as different from each other as possible to have more meaningful clustering.

Classification vs. clustering

Let us understand how classification in Supervised Learning is different from clustering in Unsupervised Learning.

Classification

In Supervised Learning our model learns a method to predict the instance class from a pre-labeled or classified instance.

Clustering

In Unsupervised Learning, our model tries to find a natural grouping of instances for a given unlabeled data.

How do we define good clustering algorithms?

High-quality clusters can be created by reducing the distance between objects in the same cluster known as intra-cluster minimizing and increasing the distance to objects in the other cluster known as inter-cluster maximization.

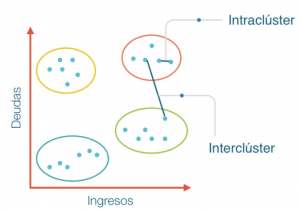
Intracluster minimization: The closer objects are to a group, the more likely they are to belong to the same group.

Intercluster maximization: this makes the separation between two groups. The main goal is to maximize the distance between two clusters.

Evaluation Metrics

The main goal of clustering is not only to create clusters, but also to create good and meaningful clusters, we saw that in the example above.

Here, we used only two features and therefore it was easy for us to visualize and decide which of these clusters is better.

Unfortunately, that’s not how real-world scenarios work. We’ll have a bunch of features to work with.

Let’s take the example of bank customer segmentation again, we will have characteristics such as income, occupation, gender, age and many more. Visualizing all these features together and deciding on better and more meaningful clusters would not be possible for us.

This is where we can make use of evaluation metrics. Let’s discuss some of them and understand how we can use them to assess the quality of our clusters.

Inertia

You remember the first property of groups that we covered earlier. This is what inertia evaluates. It tells us how far apart the points are within a group. So inertia actually computes the sum of all points within a cluster from the centroid of that cluster.

We calculate this for all clusters and the final inertia value is the sum of all these distances. This distance within the clusters is known as the intra-cluster distance. So, inertia gives us the sum of the intra-cluster distances.

Now, what do you think should be the value of inertia for a good group? Is a small initial value good or do we need a larger value? We want the points within the same group to be similar to each other, therefore the distance between them should be as low as possible.

Taking this into account, we can say that the lower the inertia value, the better our clusters are.

Dunn Index

Now we know that inertia tries to minimize the distance between clusters, trying to make clusters more compact. If the distance between the centroid of a cluster and the points in that cluster is small, it means that the points are closer to each other. Therefore, inertia makes sure that the first property of clusters is satisfied. But he doesn’t care about the second property, that the different groups are as different as possible.

This is where the Dunn Index can come into action.

Along with the distance between the centroid and the points, the Dunn index also takes into account the distance between two groups. This distance between the centers of two different clusters is known as interclusters. Let’s look at the Dunn’s index formula:

The Dunn index is the ratio between the minimum distance between clusters and the maximum distance between clusters.

We want to maximize the Dunn index. The more the value of the Dunn index, the better the clusters.

Let’s understand the intuition behind Dunn’s index:

• To maximize the value of the Dunn index, the numerator must be maximum. Here, we are taking the minimum of the distances between the clusters. Therefore, the distance between the closest clusters must be greater, which will eventually ensure that the clusters are far from each other.
• Also, the denominator must be minimal to maximize the Dunn index. Here, we are taking the maximum intracluster distances. Once again, the intuition is the same here. The maximum distance between the centers of the clusters and the points must be minimal, which will eventually ensure that the clusters are compact.

Clustering applications in the real world

Clustering is a widely used technique in industry. Actually, it is being used in almost every domain, from banking to recommendation engines, from document aggregation to image segmentation.

Customer segmentation

We have already discussed it before, one of the most common applications of clustering is customer segmentation. And it’s not limited to banking. This strategy cuts across all functions, including telecommunications, e-commerce, sports, advertising, sales, etc.

Document grouping

This is another common application of clustering. Suppose you have several documents and you need to group similar documents together. Clustering helps us group these documents so that similar documents are in the same groups.

Image segmentation

We can also use clustering to perform image segmentation. Here, we try to match similar pixels in the image. We can apply clustering to create clusters with similar pixels in the same group.

recommendation engines

Clustering can also be used in recommendation engines. Let’s say you want to recommend songs to your friends. You can look at the songs that person likes and then use clustering to find similar songs and finally recommend the most similar songs.

These are just some applications, there are many more that you surely use on a daily basis.

This is just a brief explanation about clustering in the following posts we will be explaining the algorithms within this type of Unsupervised Learning.